Ibrahim Kurban OzaslanI am a PhD candidate in Electrical and Computer Engineering at University of Southern California (USC), working with Mihailo Jovanovic. My PhD research aims to develop a system-theoretic framework for designing and analyzing optimization algorithms using tools from robust control theory.
Prior to joining USC, I received my BSc and MSc degrees
Email / Google Scholar / Github / LinkedIn / CV |
|
|
Currently, I am investigating Nevanlinna-Pick interpolation to uncover fundamental performance limits in constrained optimization problems and to design algorithms that can operate near these limits. This line of research naturally extends to the optimization of structured nonconvex-nonconcave minimax problems with applications to robust machine learning. Beyond the theoretical foundations, I am also exploring how this boundary-pushing philosophy can inform controller design for autonomous systems. Stay tuned—updates will follow soon! Interests: Optimization, Control Theory, Machine Learning, Robotics |
Journal Publications
|
Stability of primal-dual gradient flow dynamics for multi-block convex optimization
Submitted to IEEE Transactions on Automatic Control, 2024 arXiv Single-loop gradient-based algorithm for solving multi-block convex optimization problems——convergence guarantees under much weaker assumptions than existing methods including ADMM, PG-EXTRA, Condat-Vu, Champolle-Pock, and many more! |
|
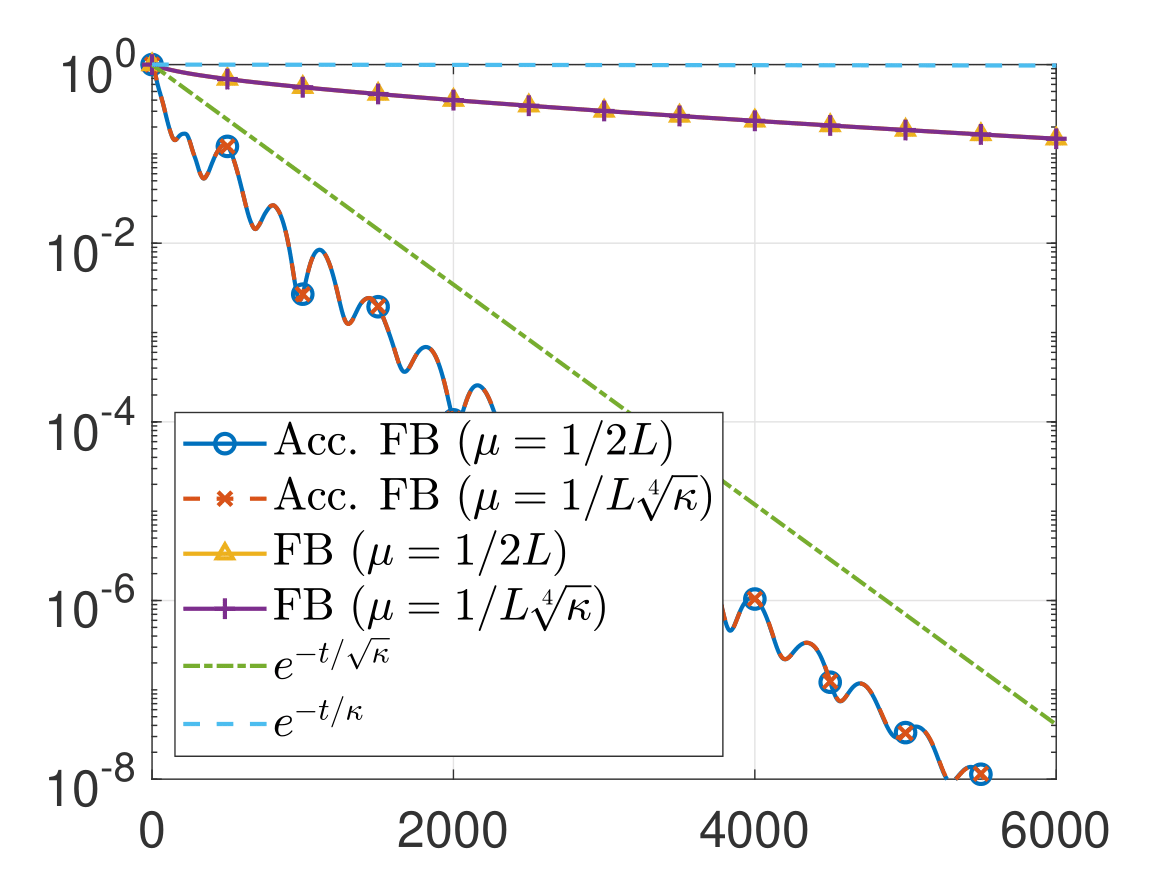
Accelerated forward-backward and Douglas-Rachford splitting dynamics
Automatica, 2024 Elsevier / arXiv Optimal rates for accelerated variants of FB and DR splittings in nonsmooth convex problems using Popov’s Lyapunov function——a control-theoretic alternative to Nesterov’s estimate sequences proof technique with ties to Popov’s frequency-domain stability criterion! |
|
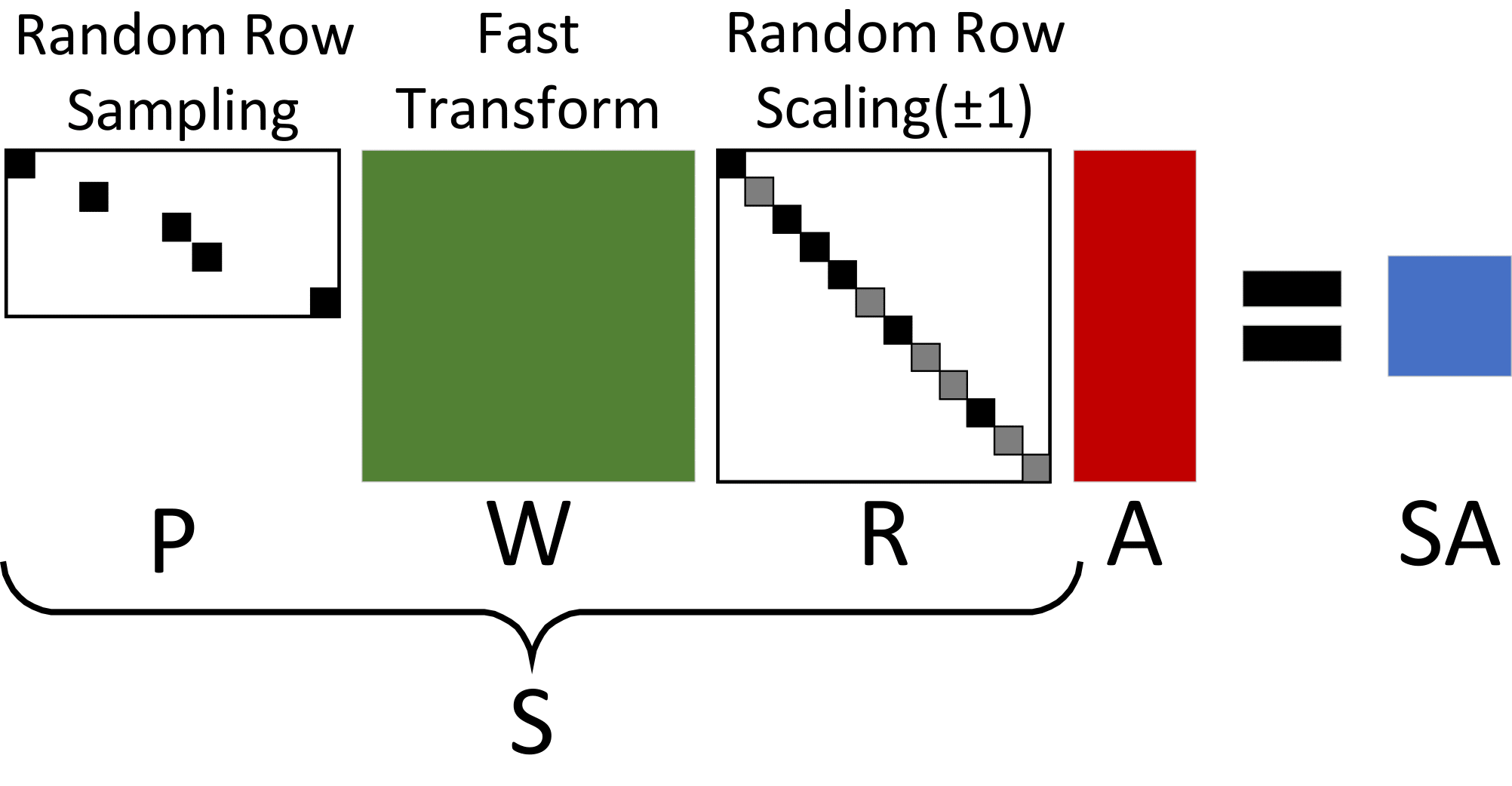
M-IHS: An accelerated randomized preconditioning method avoiding costly matrix decompositions
Linear Algebra and its Applications, 2023 Elsevier / arXiv / Github An elegant interplay between random projections and momentum-based acceleration led to development of a randomized preconditioning method with provable convergence guarantees and computational savings——stronger theoretical results and better numerical performance than popular methods like Blendenpik and LSRN! |
|
Computing stabilizing feedback gains via a model-free policy gradient
IEEE Control System Letters, 2022 IEEE / PDF Model-free policy-gradient method to compute a stabilizing controller for linear systems with unknown dynamics——convergence in finite number of iterations with high probability along with a sharp sample complexity analysis! |
Conference Publications
|
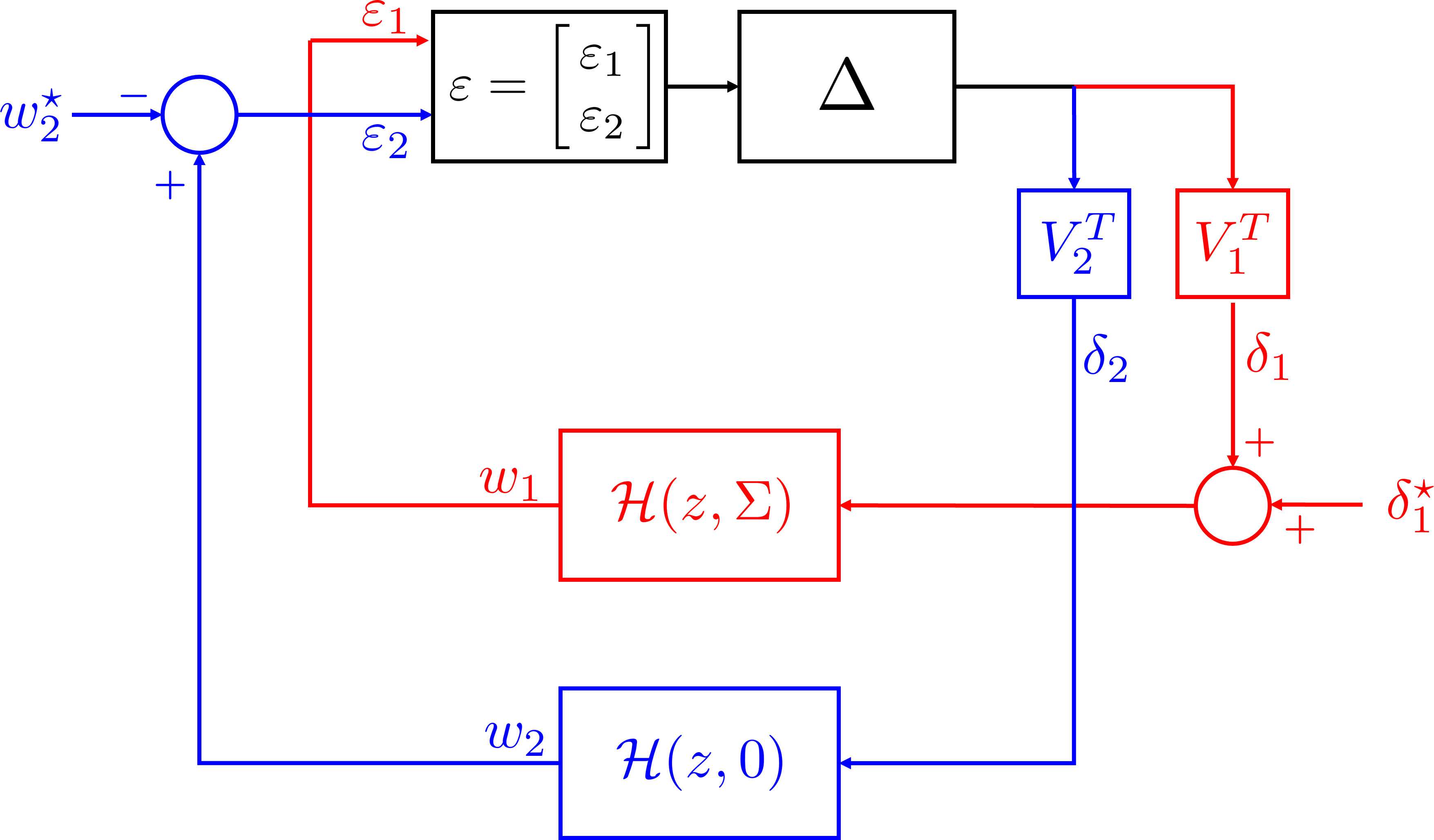
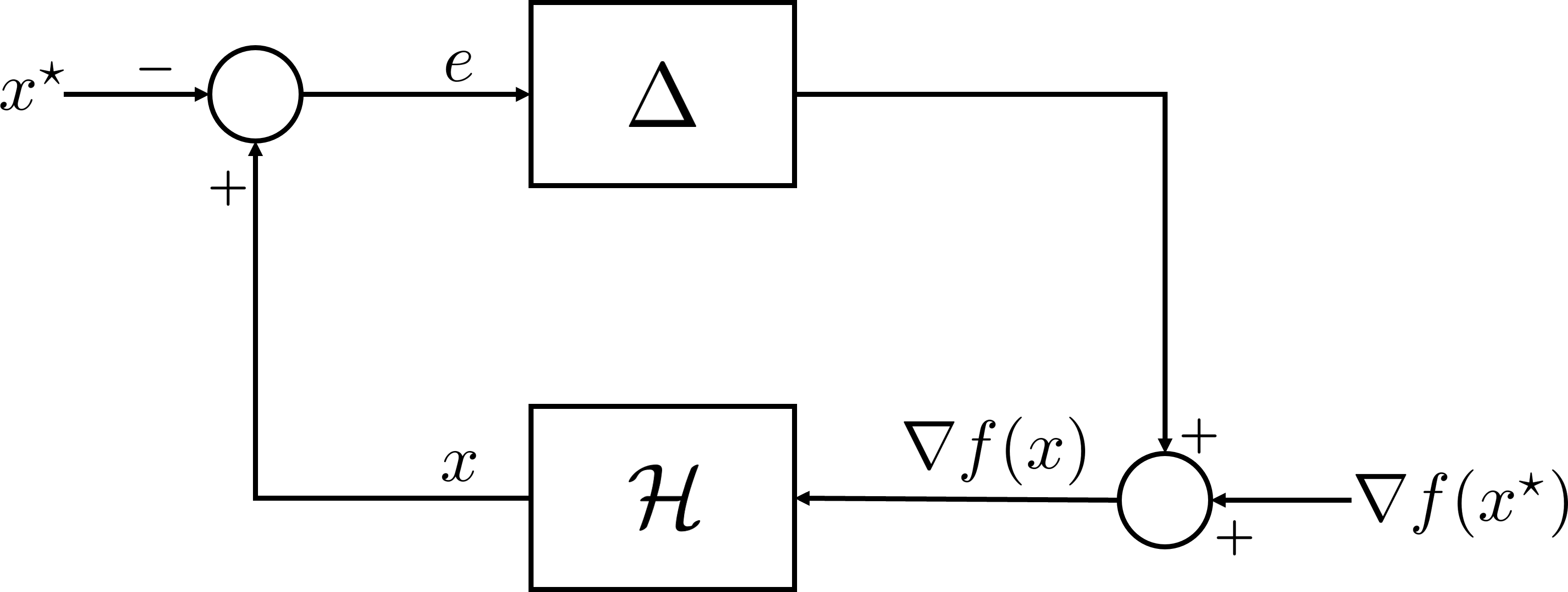
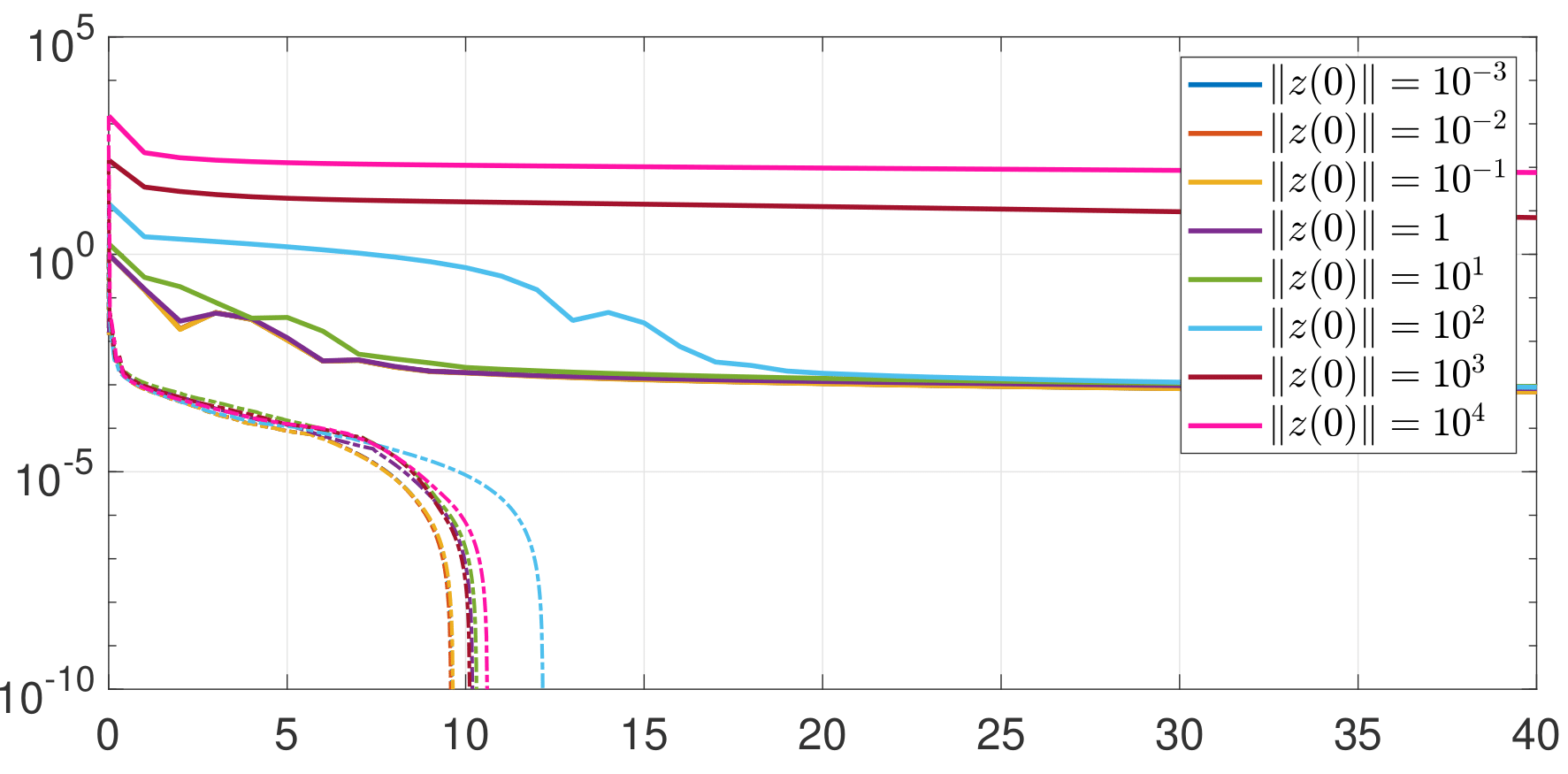
Automated algorithm design for convex optimization problems with linear equality constraints
Submitted to IEEE Conference on Decision Control (CDC), 2025 A robust control perspective on optimization——novel combination of interesting ideas such as Nevanlinna-Pick interpolation, loop transformation, internal model principle, circle criterion, and gain margin optimization! |
|
From exponential to finite/fixed-time stability: Applications to optimization
IEEE Conference on Decision Control (CDC), 2024 IEEE / arXiv Systematic procedure to turn exponential stability into finite-time stability——Why settle for accelerated asymptotic convergence when you can achieve convergence in finite time? Check out our applications to optimization! |
|
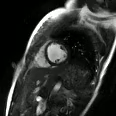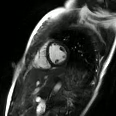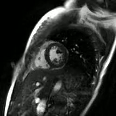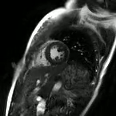
Dynamic Mode Decomposition enables low-latency high temporal resolution reconstruction for
golden-angle spiral real-time MRI
ISMRM, 2024 (awarded Summa Cum Laude) ISMRM Non-iterative online image reconstruction technique for real-time MRI using system identification——no need to wait collecting all data or run long iterations! |
|
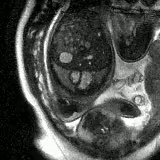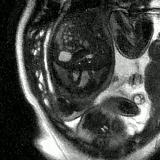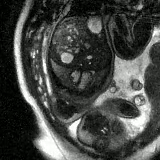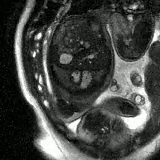
Dynamic Mode Decomposition (DMD) Cardiac Phase Estimation for adult and fetal real-time MRI
ISMRM, 2024 (awarded Summa Cum Laude) ISMRM Fast, image-based cardiac phase estimation using DMD——no ECG or heart rate assumptions, minimal user input, works even in challenging fetal imaging scenarios! |
|
Tight lower bounds on the worst-case convergence rate of primal-dual dynamics for equality constrained
convex problems
IEEE Conference on Decision Control (CDC), 2023 IEEE / PDF Provably optimal convergence rate for Gradient Decent-Ascent using KYP (positive-real) Lemma——significant improvement upon the best known results! |
|
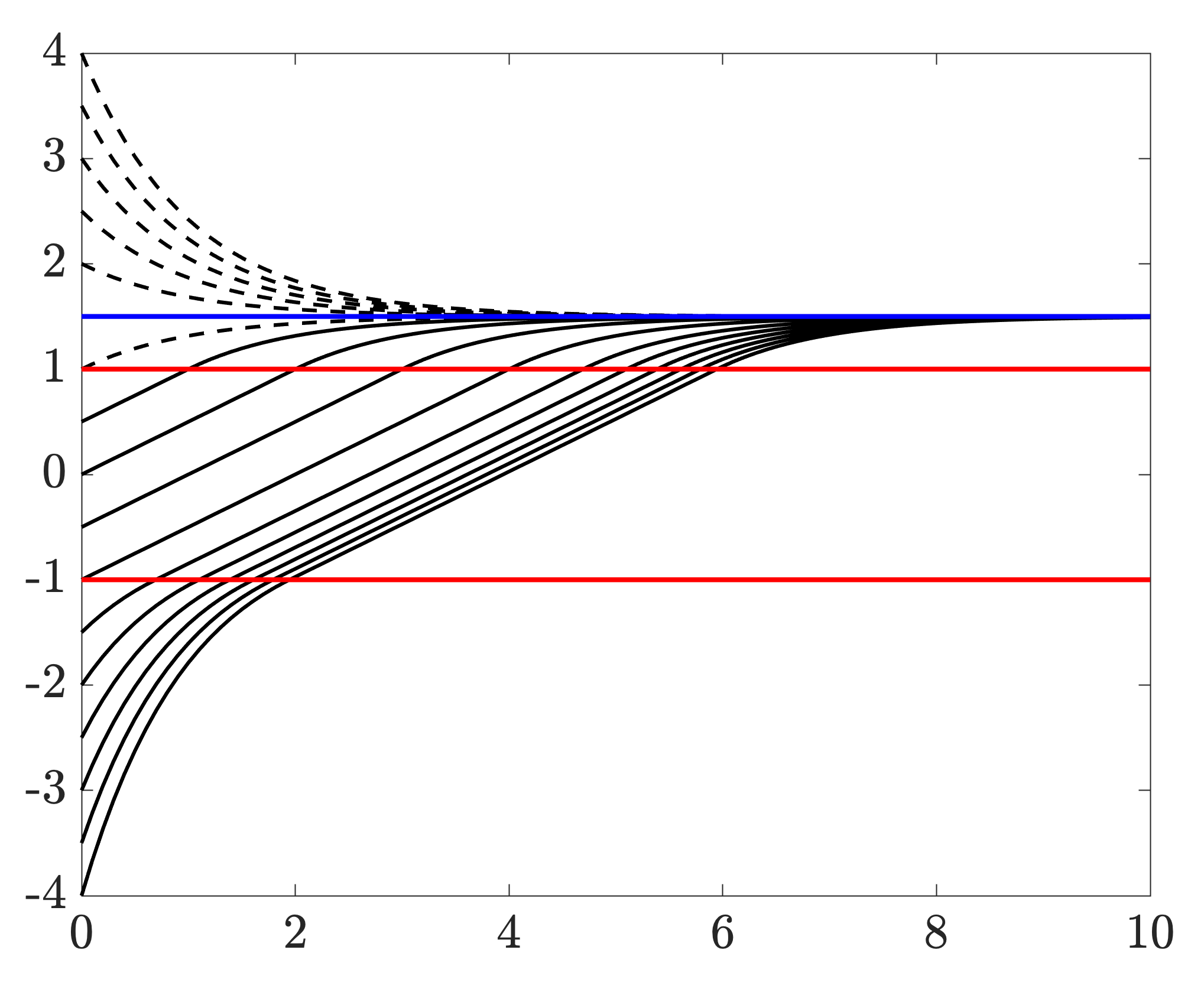
On the global exponential stability of primal-dual dynamics for convex problems with linear equality
constraints
American Control Conference (ACC), 2023 IEEE / PDF Eliminated a common assumption on the constraint matrix for linear convergence of Gradient Descent-Ascent in smooth strongly convex problems with equality constraints! |
|
Exponential convergence of primal-dual dynamics for multi-block problems under local error bound
condition
IEEE Conference on Decision Control (CDC), 2022 IEEE / PDF A novel Lyapunov function based on Lagrangian dual problem——exponentially fast convergence with no assumption on the constraint matrices and no constraint qualification! |
|
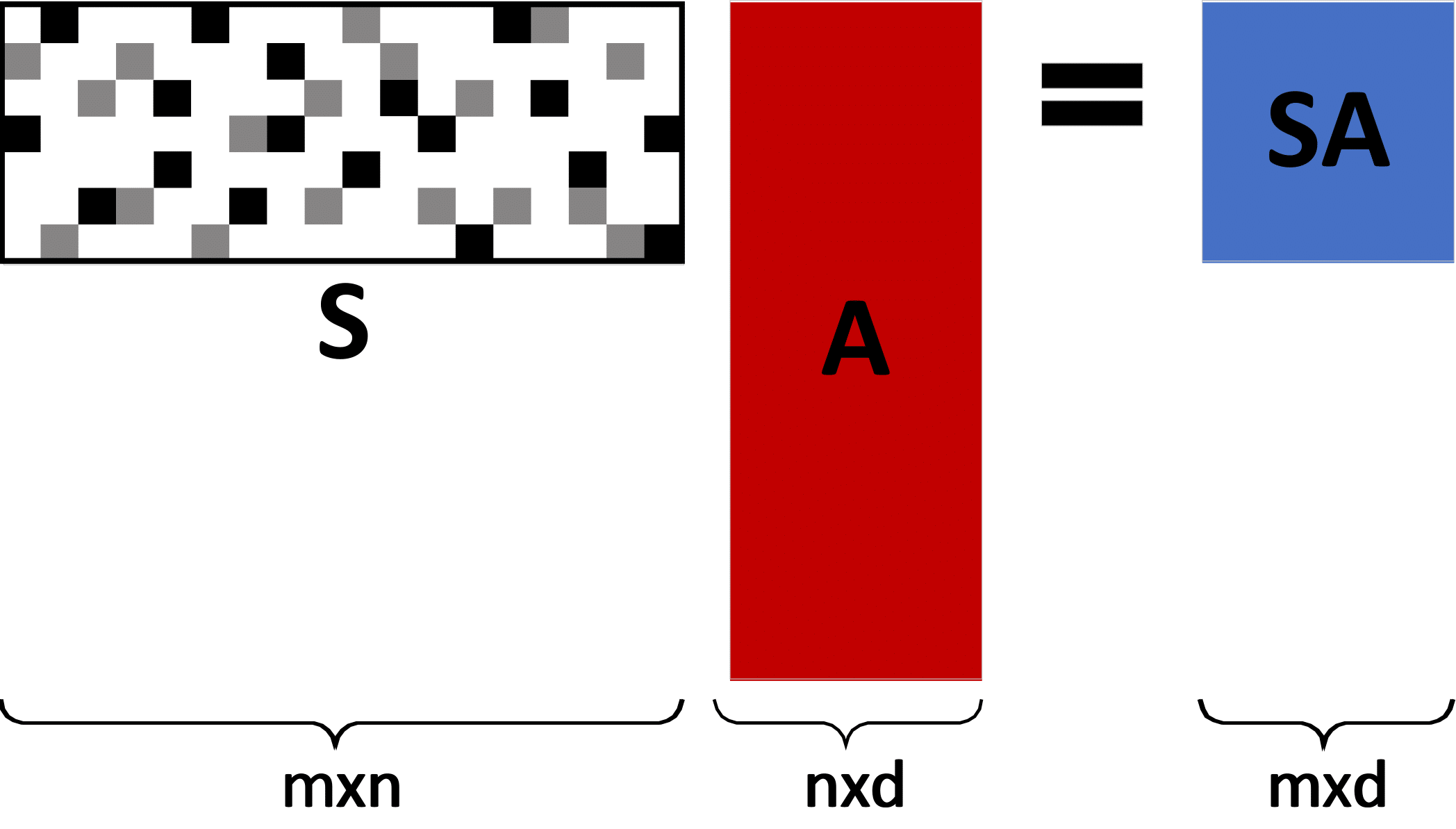
On the asymptotic stability of proximal algorithms for convex optimization problems with multiple
non-smooth regularizers
American Control Conference (ACC), 2022 IEEE / PDF Asymptotic convergence for a single-loop, gradient-based primal-dual method in multi-block convex problems——looking for a first-order method for general convex programs? Check out our novel approach! |
|
Iterative Hessian sketch with momentum
IEEE ICASSP, 2019 IEEE / PDF Novel linear system solver based on ideas from high dimensional statistics——significant computational savings over traditional Krylov Subspace methods such as conjugate gradient, LSQR, Chebyshev iterations and so on! |
|
Fast and robust solution techniques for large scale linear system of equations
IEEE Signal Processing and Communications Applications, 2019 IEEE / PDF Hybrid solver for ill-posed linear inverse problems——tired of manually tuning regularization parameters? Our approach automatically adjusts them during the iterations! |
Master's Thesis
|
Fast and Robust Solution Techniques for Large Scale Linear Least Sqaures Problems
Bilkent University, 2020 Thesis / Slides Developed a family of solvers for large-scale linear inverse problems——led to a journal paper, a technical report, two conference papers, and an invited talk! |